Let's Make a CPU: Part 1 - In the beginning there was a Transistors
by dweller - 2017-03-09
If you missed the introductory post, head here: Part 0.
In order to make a CPU we need to start from somewhere. The 0th level of abstraction here is physics (at least to our understanding), but I think that’s too low. Let’s skip that, let’s also skip electrical engineering and head straight into logic, Boolean logic that is. But before we do that I do feel the need to talk about the building block of it all.
Meet the transistor.

Transistors are very useful, before them we used cogs, relays, vacuum tubes. Obviously each one was an improvement but they were still slow as heck. But what is a transistor?
A transistor is a semiconductor device used to amplify or switch electronic signals and electrical power.
from Wikipedia
But for our purposes just think of it as a switch, you know, like the one you are using to turn on or off a light bulb. Except it’s not mechanical, and can switch thousands times per second.
There are many types of transistors, but we only care about P-type and N-type. Essentially in N-Type you need to apply current to let current flow in the gate (close the gate) and in P-type it’s the reverse.
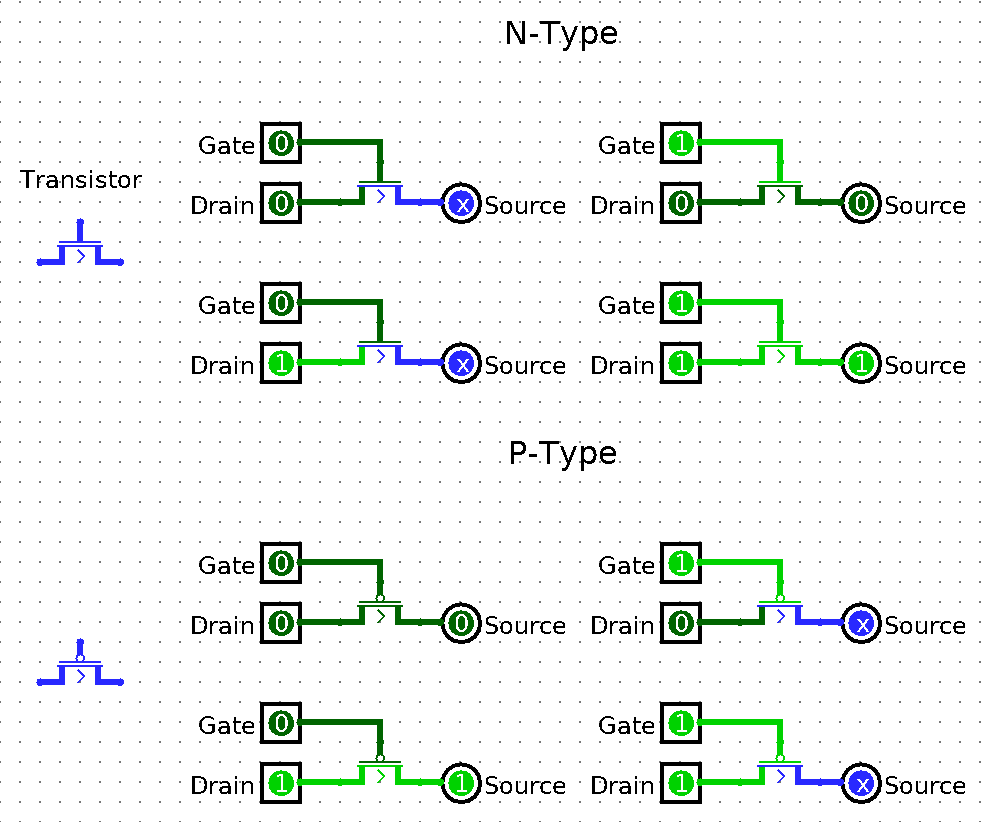
Quick tour of Logisim:
- Squares are inputs;
- Circles are outputs;
- Dark green = false/0/low current;
- Bright green = true/1/high current;
- Blue = no current;
- Red = error.
Notice that source is an output. There’s a physical explanation of that, but we don’t need to care about it, since we are dealing with logic only, not current.
So how can a switch be used to do computation? Well, enter Boolean algebra. The same one that you use in high-level languages to check conditions! With a couple of transistors we can create familiar to us operations like NOT, OR, and an AND.
But before we do that, let’s look at one property in Boolean algebra - functional completeness.
In logic, a functionally complete set of logical connectives or Boolean operators is one which can be used to express all possible truth tables by combining members of the set into a Boolean expression.
from Wikipedia
To simplify, some set of Boolean operators can emulate all the other ones. For example, you can create all the operators using only AND and NOT. Better yet single NAND (NOT AND) operation is functionally complete! This means that by creating NAND gate with transistors we can then use the same part to create everything else.
“Hold on a sec, what’s a ‘gate’?” - some of you might ask. In a nutshell it’s some device that performs some Boolean function. A NAND gate in this case is some device that takes 2 or more inputs performs NOT AND operation on them and return an output.
So why would we want to make everything out of one gate? Well there are a lot of reasons actually, and to be honest I don’t know them all. Here’s the gist: smaller sizes, lower power consumption, less signal noise and I guess process streamlining.
But enough with words! Let’s see it all in action!
First we need to define what we want our gate to do. There are a bunch of representations of Boolean functions, but I think the most readable at a glance are truth tables. You put all your possible inputs into columns on the left, and your corresponding outputs on the right, and voila!
| a | b | out |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
As we can see we need to output 1 in all cases except when both inputs are 1, so let’s build this gate using only transistors.
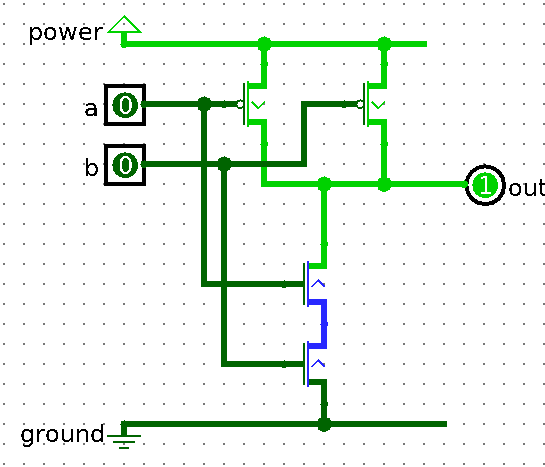
There are many ways to do this, I chose the CMOS NAND gate implementation, but it doesn’t really matter in our case.
Let’s analyze the circuit using Logisim. We can ask it to generate truth table and algebraic expression which we can use to make sure our gate is doing what we want. (Project -> Analyze Circuit -> Table)
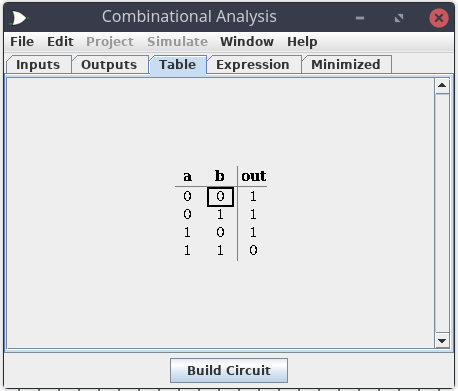
Success! We created our first gate! Now finally we can leave this layer of abstraction and move on!
Next time we will create all the other gates and make our first computation!
I would also highly recommend you to play around in Logisim, see what sorts of things you can create with just few basic components!
P.S. if you find any errors, or want to give me some feedback, feel free to send me an email